GCSE maths breakdown: Topics, learning objectives & sample questions

Why maths matters for GCSE success

GCSE Maths is one of the most important GCSE subjects; it’s required for most college courses, apprenticeships, and jobs. Many sixth forms and further education providers want at least a grade 4, which is a standard pass. Some A level subjects, like sciences or economics, may need a grade 6 or higher.

A strong GCSE Maths grade also opens the door to careers in:

• Engineering, architecture, and construction

• Finance, accountancy, and data analysis

• Teaching, science, and healthcare

• Tech roles like programming and software development

Overview of the 2026 GCSE Maths exam

The 2026 GCSE Maths exams will follow the current rules from the main exam boards: AQA, Edexcel, OCR, and WJEC. Each board assesses the same core content, with slight variations in question phrasing and structure.

Exam structure:

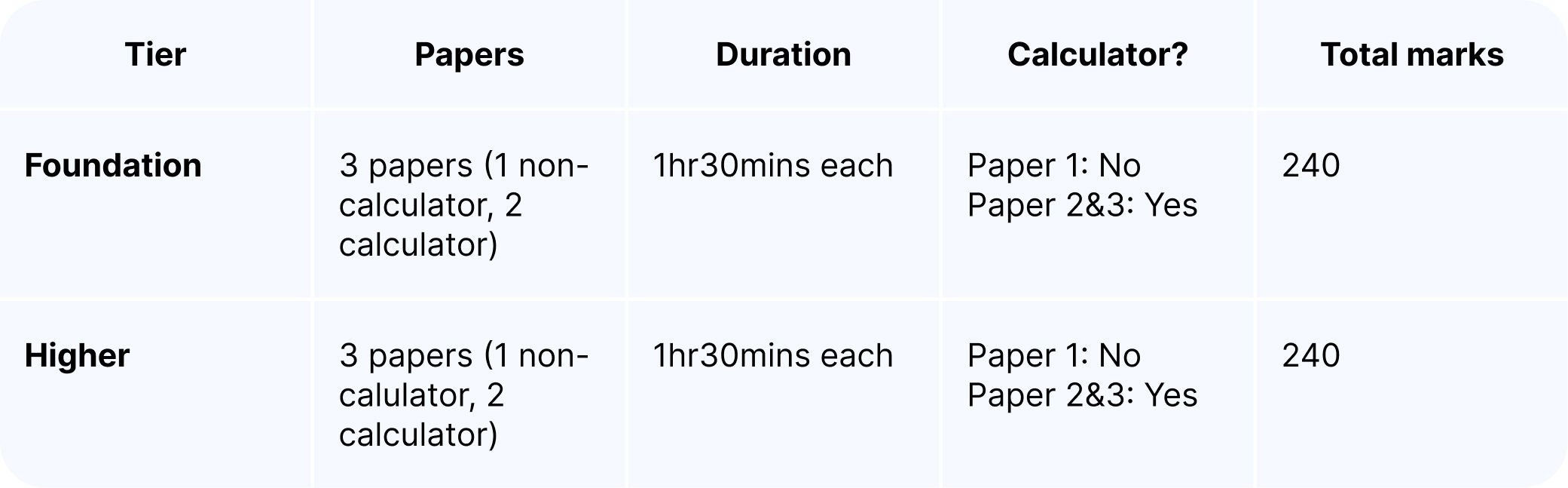
Core GCSE Maths topics (Foundation & Higher)

GCSE Maths content is split across six broad domains. Here’s what students need to cover, with Foundation and Higher tier examples to show how the difficulty can vary.

1. Number

Learning objectives:

• Apply place value, rounding, and estimation

• Work with fractions, decimals, and percentages

• Use ratio and proportion

• Apply powers, roots, and standard form

Sample question:

Foundation:

What is 25% of 160?

Answer: 40

Higher:

Write 3,600,000 in standard form and evaluate: (3.6 × 10⁶) ÷ (1.2 × 10³)

Answer: 3 × 10³

2. Algebra

Learning objectives:

• Simplify expressions, solve equations, and rearrange formulae

• Plot graphs and interpret relationships

• Work with sequences, inequalities, and algebraic proof

Sample questions:

Foundation:

Solve: 2x + 5 = 17

Answer: x = 6

Higher:

Factorise: x² − 5x − 24

Answer: (x − 8)(x + 3)

3. Ratio, proportion and rates of change

Learning objectives:

• Solve problems using direct and inverse proportion

• Use percentages in context (e.g. growth/decay)

• Interpret compound measures like speed and density

Sample questions:

Foundation:

A recipe uses 300g of flour for 4 servings. How much flour is needed for 6 servings?

Answer: 450g

Higher:

A car travels 180 km in 2 hours 15 minutes. What is its average speed in km/h?

Answer: 80 km/h

4. Geometry and measures

Learning objectives:

• Use angle facts, properties of shapes, and symmetry

• Apply Pythagoras’ theorem and trigonometry

• Calculate perimeter, area, volume, and surface area

Sample questions:

Foundation:

Find the perimeter of a rectangle with sides 5 cm and 8 cm.

Answer: 26 cm

Higher:

A triangle has sides 7 cm and 9 cm with an included angle of 60°. Use the cosine rule to find the third side.

Answer: c² = 7² + 9² − 2×7×9×cos(60) → c ≈ 7.6 cm

5. Probability

Learning objectives:

• Understand and calculate probabilities from tables, lists, and diagrams

• Use Venn diagrams and tree diagrams

• Know the laws of probability (mutually exclusive and independent events)

Sample questions:

Foundation:

A bag contains 5 red balls and 3 blue balls. What is the probability of picking a red ball?

Answer: 5/8

Higher:

Two biased coins are flipped. The probability of heads on each is 0.6. Find the probability of getting exactly one head.

Answer: 0.6 × 0.4 + 0.4 × 0.6 = 0.48

6. Statistics

Learning objectives:

• Interpret and create charts, graphs, and tables

• Calculate averages and range

• Understand sampling, correlation, and distributions

Sample questions:

Foundation:

Find the median of: 3, 7, 8, 12, 15

Answer: 8

Higher:

A grouped frequency table shows the number of hours 20 students revised. Estimate the mean number of hours.

(A frequency table would be provided)

Answer: Use midpoints × frequency, then divide total by 20

Key differences between Foundation and Higher tier

Who should take Foundation?

• Students aiming for a secure pass (grade 4 or 5)

• Those who may find abstract problem-solving or algebraic manipulation more difficult

• Learners who benefit from clear, structured questions

Who should take Higher?

• Students consistently working at grade 6 or above in class assessments

• Those hoping to study A level Maths or other maths-related subjects

• Learners who enjoy reasoning, spotting patterns, and tackling challenging problems

If a student is comfortably working at grade 6+ and enjoys the subject, Higher tier can unlock more opportunities. However, aiming for a strong result on Foundation (grade 5) is often better than risking a low grade on Higher.

Always talk to your teacher or tutor to find the best option. Exam boards let schools enter students for either tier based on their performance during the course.

Effective Maths revision strategies

Revising for GCSE Maths is most effective when it’s consistent, targeted, and varied. These strategies can help build confidence and improve results, whether preparing independently, supporting a student, or guiding a class.

Start with your weakest topics.

• Focus first on areas that need the most improvement. Identifying these early through practice papers, quizzes, or feedback helps ensure no gaps remain by exam time.

Cover all six content areas regularly.

• Rather than revising one topic for an extended period, revisit each of the six main areas (Number, Algebra, Ratio, Geometry, Probability, and Statistics) often. This keeps skills fresh and supports problem-solving across the whole paper.

Learn from worked examples.

• Reviewing step-by-step solutions helps clarify methods and reasoning. Once confident with the approach, practise similar questions independently to strengthen recall and application.

Keep a concise formula sheet.

• Some formulae are provided in the exam, but knowing them from memory is a real advantage. A single, personalised sheet can be used for quick reference during revision sessions.

Practise non-calculator techniques.

• Paper 1 is non-calculator, so fluency with mental maths, estimation, and written methods is important. Regular practice without a calculator helps develop speed and accuracy.

With the right strategy and tools, GCSE Maths doesn’t need to be stressful.

Little and often is the key. Keep revising regularly, build confidence with past questions, and remember, steady progress adds up. Every small step moves you forward. Whether you want to pass or get top marks, knowing what is on your exam gives you a strong advantage.